Type I and Type II Errors (Jump to: Lecture | Video )

Here's the example from the previous lecture:

School District A states that its high schools have an 85% passage rate on the High School Exit Exam. A new school was recently opened in the district, and it was found that a sample of 150 students had a passage rate of 88%, with a standard deviation of 4%. Does this new school have a different passage rate than the rest of School District A? Answer this question using an alpha level of .05.

Figure 1.

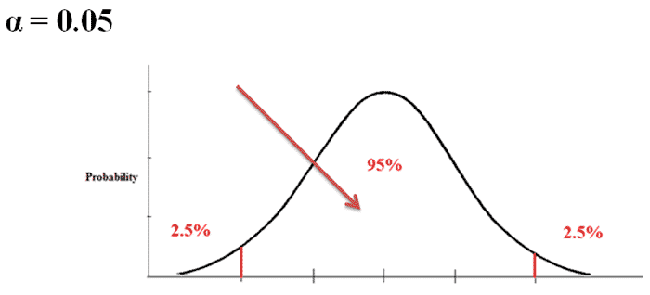
We're testing to see if the statistic we calculate (for example "z") is within the 95% range we expect it to be. If it is, we will conclude that what we’re testing (usually the mean) is right where we expect it to be, so we will retain (keep) the null hypothesis.

Figure 2.

If the statistic we calculate is outside of that range, we will conclude that what we’re testing is not where we expect it to be, so it’s very likely that the null hypothesis is not true. So, we reject the null hypothesis and say that the alternative hypothesis is true.

In reality, the school we sampled from either has a passage rate of 85% (our null hypothesis) or it has something different than 85% (the alternative hypothesis). We haven’t measured the entire school, we only measured a sample of students. The decision we make will be based on the characteristics of the sample we’ve taken and what we know about the probabilities associated with the normal curve.

Because statistics don’t always accurately reflect the values of parameters, the decision we make may or may not accurately reflect reality. There are four possible outcomes, two of which are good, and two of which are errors:

Outcome 1: We reject the Null Hypothesis when in reality, it is false. GOOD

Outcome 2: We reject the Null Hypothesis when in reality, it is true. Type I Error

Outcome 3: We do not reject the Null Hypothesis when in reality, it is false. Type II Error

Outcome 4: We do not reject the Null Hypothesis when in reality, it is true. GOOD