Repeated-Measures ANOVA (Jump to: Lecture | Video )

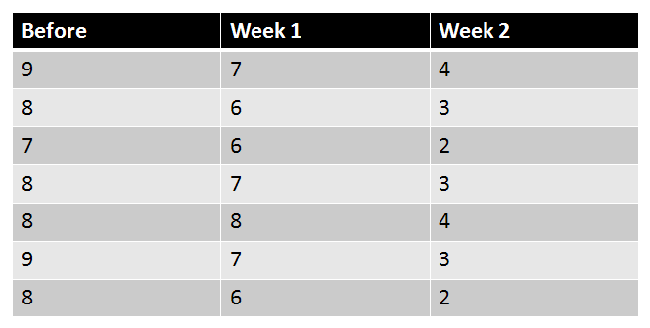
Let's perform a repeated-measures ANOVA: Researchers want to test a new anti-anxiety medication. They measure the anxiety of 7 participants three times: once before taking the medication, once one week after taking the medication, and once two weeks after taking the medication. Anxiety is rated on a scale of 1-10, with 10 being "high anxiety" and 1 being "low anxiety". Are there any differences between the three conditions using alpha = 0.05?

Figure 1.

Steps for Repeated-Measures ANOVA
1. Define Null and Alternative Hypotheses 2. State Alpha 3. Calculate Degrees of Freedom 4. State Decision Rule 5. Calculate Test Statistic 6. State Results 7. State Conclusion

Let's begin.

1. Define Null and Alternative Hypotheses

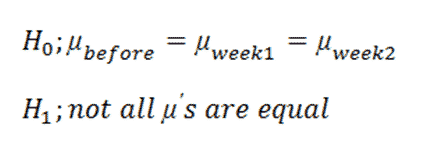
Figure 2.

2. State Alpha

Alpha = 0.05

3. Calculate Degrees of Freedom

Now we calculate the degrees of freedom using N = 21, s = 7, and a = 3. You should already recognize N. "a" refers to the number of groups ("levels") you're dealing with, and "s" refers to the number of subjects you have in each condition:

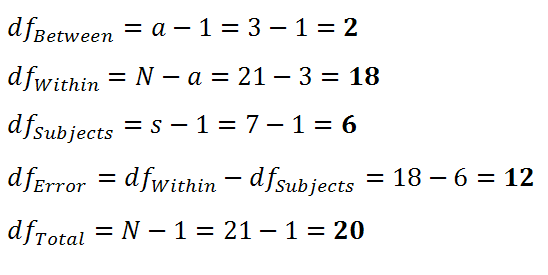
Figure 3.

4. State Decision Rule

To look up the critical value, we need to use two different degrees of freedom.

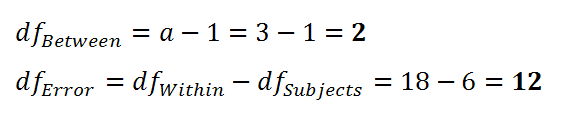
Figure 4.

We now head to the F-table and look up the critical value using (2, 12) and alpha = 0.05. This results in a critical value of 3.8853, so our decision rule is:

If F is greater than 3.8853, reject the null hypothesis.

5. Calculate Test Statistic

To calculate the test statistic, we first need to find three of five values:

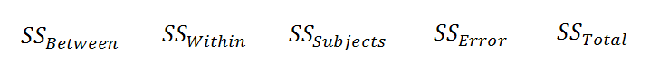
Figure 5.

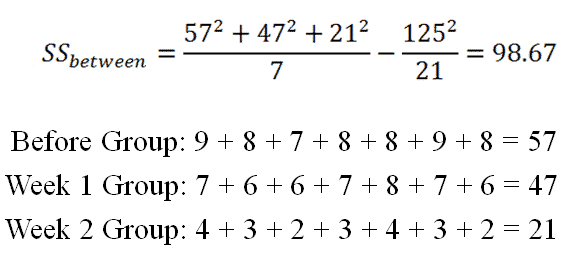
Figure 6.

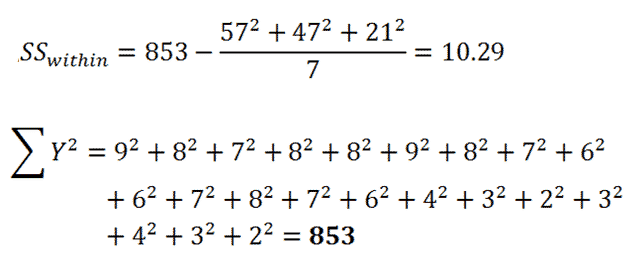
Figure 7.

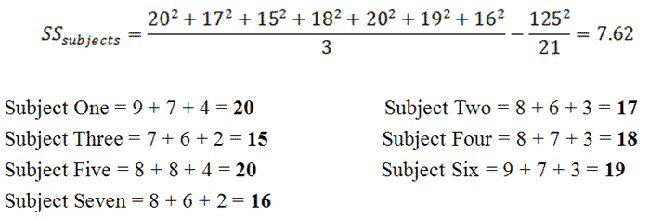
Figure 8.

All the values we've found so far can be organized in an ANOVA table:

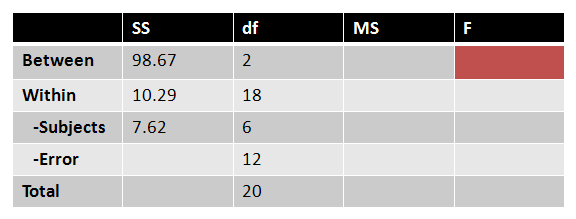
Figure 9.

We can use the three values we've already found to fill in the two unknown values:

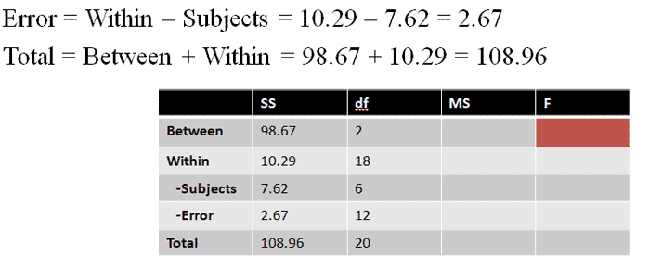
Figure 10.

Now we find each MS by diving each SS by their respective df:

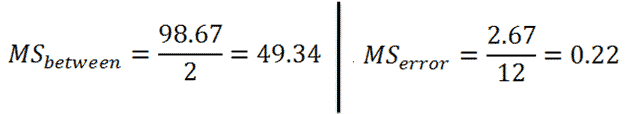
Figure 11.

And finally, we can calculate our F:

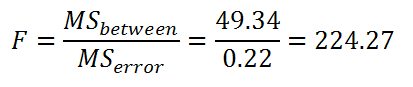
Figure 12.

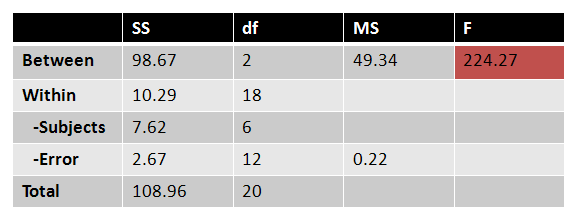
Figure 13.

6. State Results

F = 224.27

Result: Reject the null hypothesis.

7. State Conclusion

The three conditions differed significantly on anxiety level, F(2, 12) = 224.27, p < 0.05.

---