Rational Zero Theorem (Jump to: Lecture | Video )

Rational Zero Theorem
If a polynomial equation has integer coefficients, then any rational zero must be in the form of 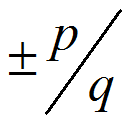where p is a factor of the constant term, and q is a factor of the leading coefficient.

Find the rational zeros of:

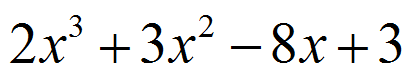
Figure 1.

First, we determine the factors of the leading coefficient and the constant:

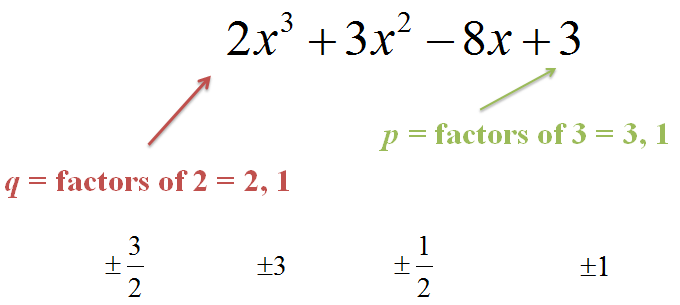
Figure 2.

Next, we perform synthetic division using each p/q term is the divisor. Any row that has no remainder is a 0 for this function.

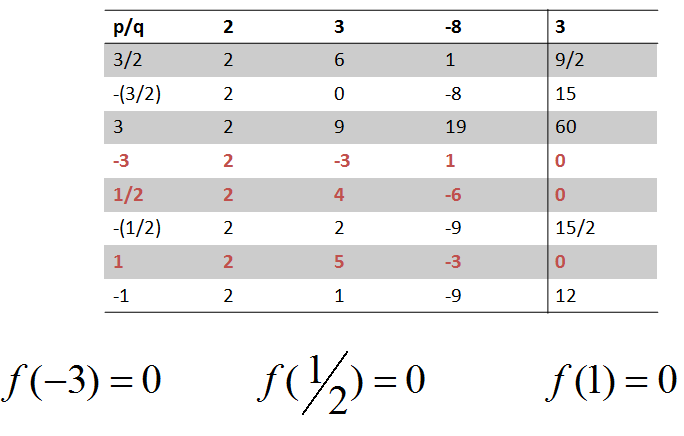
Figure 3.

The value of the function is 0 when x = -3, x = 1/2, and x = 1.