Rate of Decay (Jump to: Lecture | Video )

Imagine a glass that contains 500ml of water. If 12% of the water evaporates every hour, how long will it take for 100ml to remain?

We can solve this problem using the following equation:

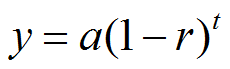
Figure 1.

y = final amount

a = initial amount

r = rate of decay

t = time

We can arrange our knowns to solve for the unknown, using the logarithmic properties we learned about recently:

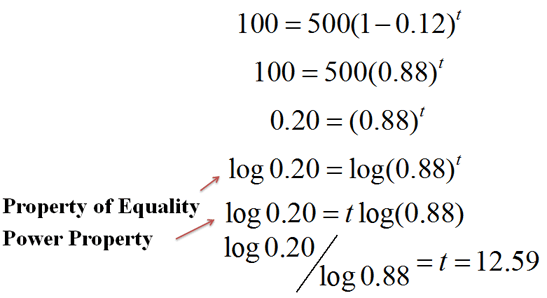
Figure 2.

It will take 12.59 hours for 100ml of water to remain.

The half-life of a radioactive substance is the time it will take for half of the substance to decay. For example, the half-life for a mass of Carbon is 5730 years.

We can solve this problem using the following equation:

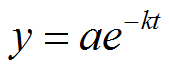
Figure 3.

What is k? That is, what is the rate of decay of Carbon?

y = final amount

a = initial amount

e = natural base

t = time

Again, we can arrange our knowns to solve for the unknown, using the logarithmic properties we learned about recently:

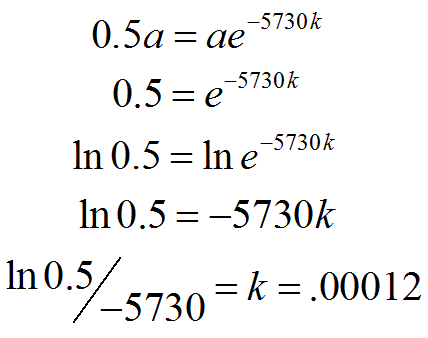
Figure 4.

The rate of decay of Carbon is k = .00012

---