Poisson Distribution/Process (Jump to: Lecture | Video )

Here's an example: At a theme park, there is a roller coaster that sends an average of three cars through its circuit every minute between 6pm and 7pm. A random variable, X, represents the number of roller coaster cars to pass through the circuit between 6pm and 6:10pm.

First, let's check if this contains a Poisson random varilable:

Is the probability of two successes in a small enough interval 0%?

YES, in a small enough interval (say, 1 second) it would be impossible for two successes (cars through the circuit) to occur.

Are the probabilities of success equal for any two intervals of equal length?

YES, between any two equal intervals (say, 6pm-6:15pm, and 6:30pm-6:45pm), the average (probability of success) remains 3 cars.

Are successes independent of successes in other intervals?

YES, a success in one interval is independent of a success in any other interval.

What is the probability that 35 cars will pass through the circuit between 6pm and 6:10pm?

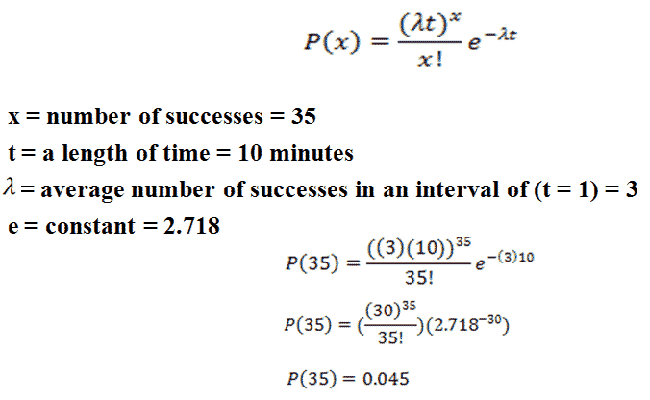
Figure 1.

The probability that 35 cars will pass through the circuit between 6pm and 6:10pm is 0.045.