Pearson’s r Correlation (Jump to: Lecture | Video )

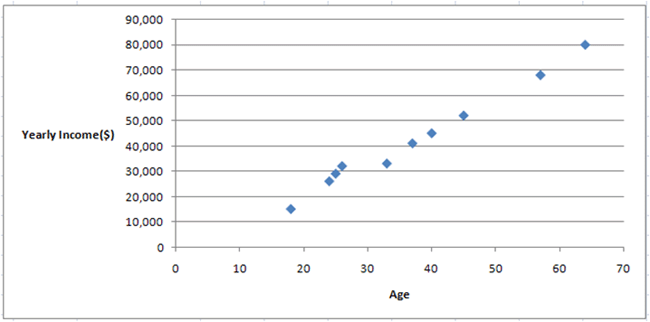
In the previous lecture on scatter plots, we made a scatter plot for some sample bivariate data and concluded that the two variables were probably related.

Figure 1.

We can use this data to calculate Pearson's r

Pearson’s r
Pearson’s r measures the strength of the linear relationship between two variables. Pearson’s r is always between -1 and 1.

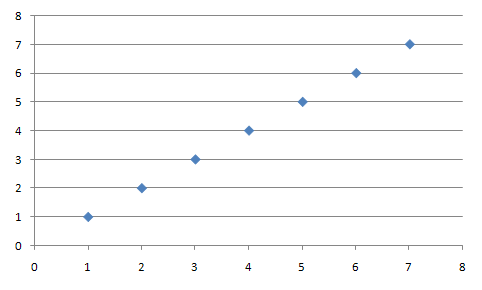
Here is a perfect positive relationship. r is equal to 1.0:

Figure 2.

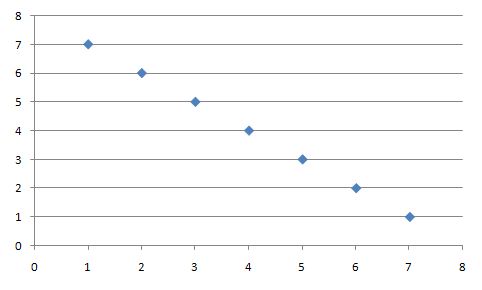
Here is a perfect negative relationship. r is equal to -1.0:

Figure 3.

Here is an example of data that has no relationship. r is somewhere close to 0.0:

Figure 4.

Pearson's r is calculated with the following equation:

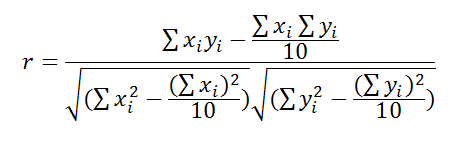
Figure 5.

Plugging in the values from our original example with ages and yearly incomes, we can calculate the following r:

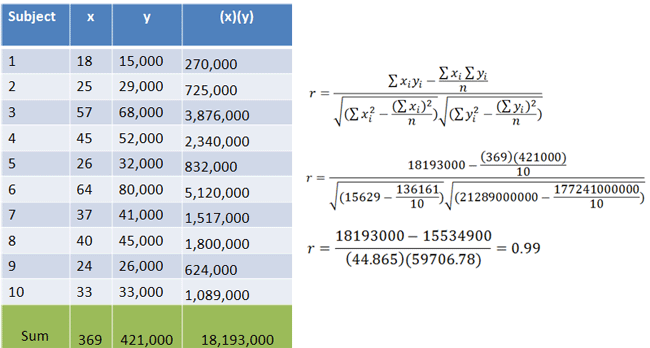
Figure 6.

This r is almost 1.0, so we can conclude that x(Age) and y(Yearly Income) have a strong positive relationship. As one increases, the other tends to increase as well.

---