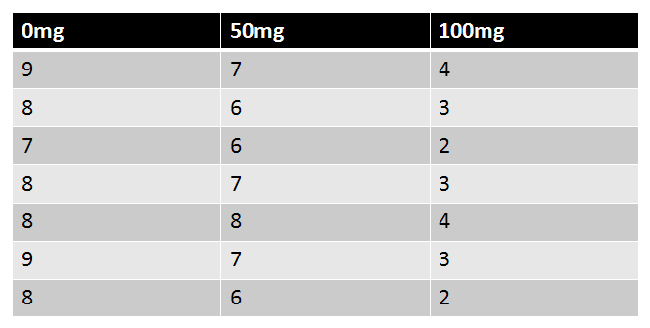
Let's perform a one-way ANOVA: Researchers want to test a new anti-anxiety medication. They split participants into three conditions (0mg, 50mg, and 100mg), then ask them to rate their anxiety level on a scale of 1-10. Are there any differences between the three conditions using alpha = 0.05?
|
Figure 1. |
|---|
| Steps for One-Way ANOVA |
|---|
|
1. Define Null and Alternative Hypotheses 2. State Alpha 3. Calculate Degrees of Freedom 4. State Decision Rule 5. Calculate Test Statistic 6. State Results 7. State Conclusion |
Let's begin.
1. Define Null and Alternative Hypotheses
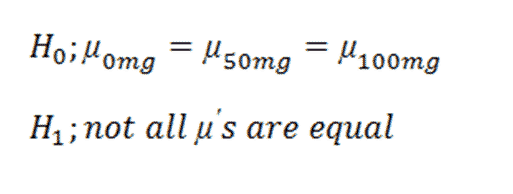
|
Figure 2. |
|---|
2. State Alpha
Alpha = 0.05
3. Calculate Degrees of Freedom
Now we calculate the degrees of freedom using N = 21, n = 7, and a = 3. You should already recognize N and n. "a" refers to the number of groups ("levels") you're dealing with:
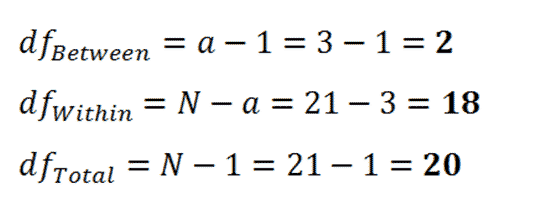
|
Figure 3. |
|---|
4. State Decision Rule
To look up the critical value, we need to use two different degrees of freedom.
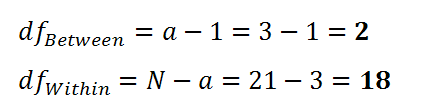
|
Figure 4. |
|---|
We now head to the F-table and look up the critical value using (2, 18) and alpha = 0.05. This results in a critical value of 3.5546, so our decision rule is:
If F is greater than 3.5546, reject the null hypothesis.
5. Calculate Test Statistic
To calculate the test statistic, we first need to find three values:
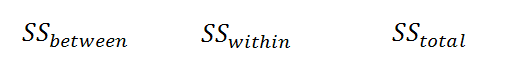
|
Figure 5. |
|---|
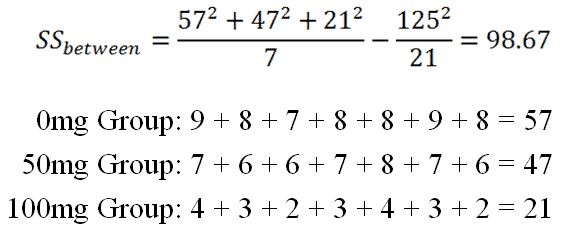
|
Figure 6. |
|---|
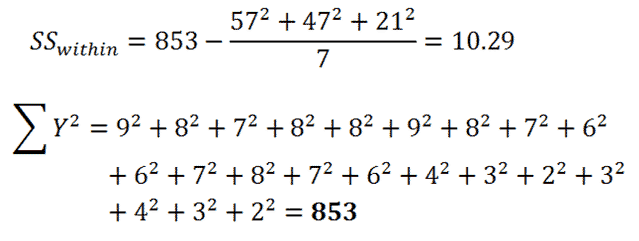
|
Figure 7. |
|---|
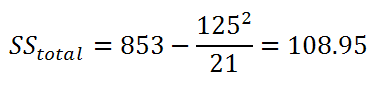
|
Figure 8. |
|---|
All the values we've found so far can be organized in an ANOVA table:
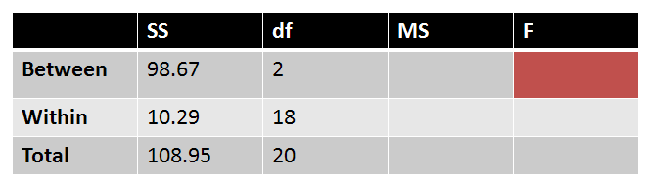
|
Figure 9. |
|---|
Now we find each MS by diving each SS by their respective df:
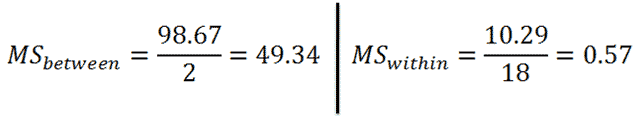
|
Figure 10. |
|---|
And finally, we can calculate our F:
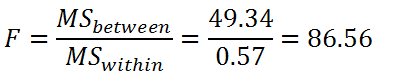
|
Figure 11. |
|---|
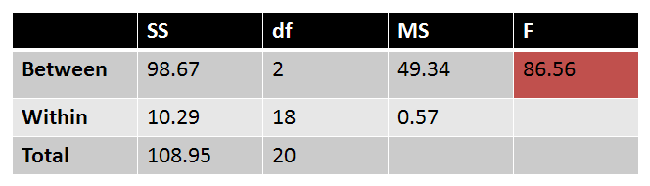
|
Figure 12. |
|---|
6. State Results
F = 86.56
Result: Reject the null hypothesis.
7. State Conclusion
The three conditions differed significantly on anxiety level, F(2, 18) = 86.56, p < 0.05.