One Sample z-Test

Navigation

Resources

One Sample z-Test (Jump to: Lecture | Video )

Let's perform a one sample z-test: In the population, the average IQ is 100 with a standard deviation of 15. A team of scientists wants to test a new medication to see if it has either a positive or negative effect on intelligence, or no effect at all. A sample of 30 participants who have taken the medication has a mean of 140. Did the medication affect intelligence, using alpha = 0.05?

Steps for One-Sample z-Test
1. Define Null and Alternative Hypotheses 2. State Alpha 3. State Decision Rule 4. Calculate Test Statistic 5. State Results 6. State Conclusion

Steps for One-Sample z-Test

1. Define Null and Alternative Hypotheses

2. State Alpha

3. State Decision Rule

4. Calculate Test Statistic

5. State Results

6. State Conclusion

Let's begin.

1. Define Null and Alternative Hypotheses

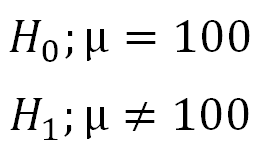
Figure 1.

2. State Alpha

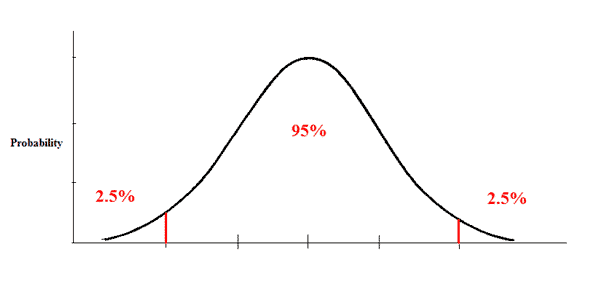
Using an alpha of 0.05 with a two-tailed test, we would expect our distribution to look something like this:

Figure 2.

Here we have 0.025 in each tail. Looking up 1 - 0.025 in our z-table, we find a critical value of 1.96. Thus, our decision rule for this two-tailed test is:

If Z is less than -1.96, or greater than 1.96, reject the null hypothesis.

4. Calculate Test Statistic

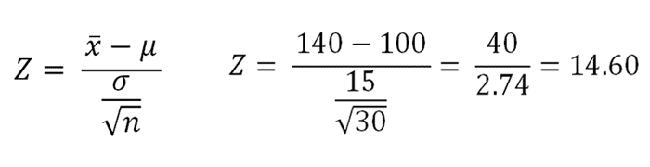
Figure 3.

5. State Results

Z = 14.60

Result: Reject the null hypothesis.

6. State Conclusion

Medication significantly affected intelligence, z = 14.60, p < 0.05.