Mean and Expected Value of Discrete Random Variables (Jump to: Lecture | Video )

Let's calculate the mean of a discrete random variable:

Below is the probability distribution for a golfer on a par 3 hole, where x = Number of Strokes to Complete Course

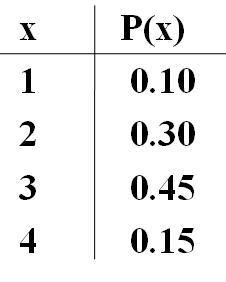
Figure 1.

The mean can be calculated by multiplying each "x" by each "P(x)", then adding the resulting values together:

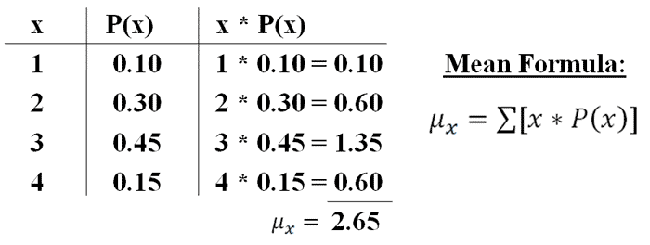
Figure 2.

Here, the mean is 2.65

The mean we just calculated of 2.65 is an expected value. If we were to take a large enough sample of this golfer’s performance on par 3 holes, we expect his mean to approach 2.65.

This is a short example of the Law of Large Numbers.