Linear Regression (Jump to: Lecture | Video )

In a previous lecture on Pearson's r, we found two sets of data to be highly correlated:

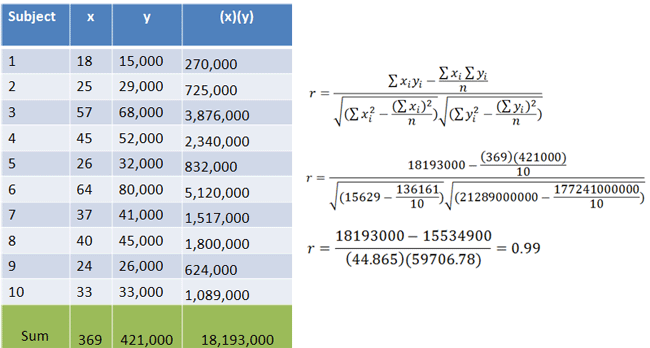
Figure 1.

If we know that two variables are strongly correlated, we can use one variable to predict the other using the following equations:

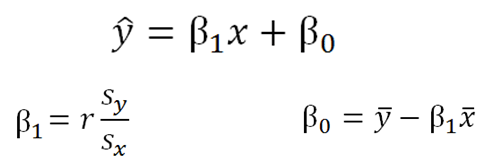
Figure 2.

Here, we first calculate beta1 and beta0 and place them in the top equation. Then, if we plug an x into the equation, we can predict what our y value will be.

The stronger your correlation (that is, the closer r is to -1 or 1), the more accurate your prediction will be.

First, we solve for beta1:

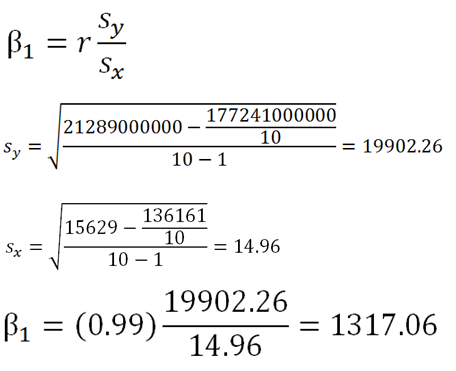
Figure 3.

We then use beta1's value to solve for beta0:

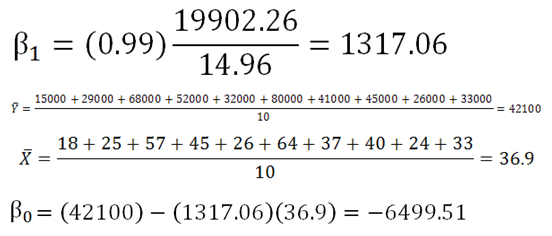
Figure 4.

Now, putting those values into the original equation, we have our completed regression equation:

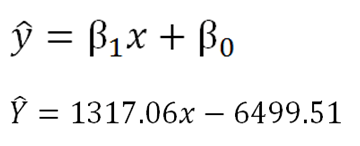
Figure 5.

Predict the yearly income of someone who is 33 years old.

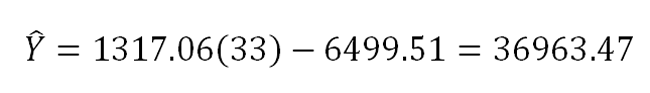
Figure 6.

We would expect someone who is 33 years old to make approximately $36,963 a year.

---