Kruskal-Wallis Test (Jump to: Lecture | Video )

Kruskal-Wallis Test
The Kruskal-Wallis Test is a version of the independent measures (One-Way) ANOVA that can be performed on ordinal(ranked) data.

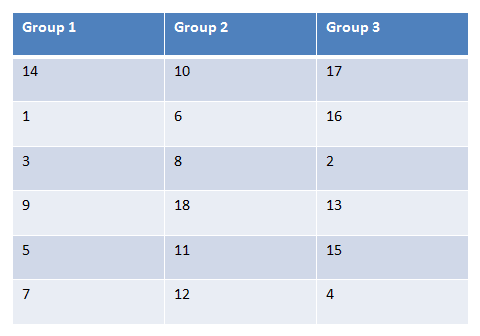
Ordinal data is displayed in the table below. Is there a difference between Groups 1, 2, and 3 using alpha = 0.05?

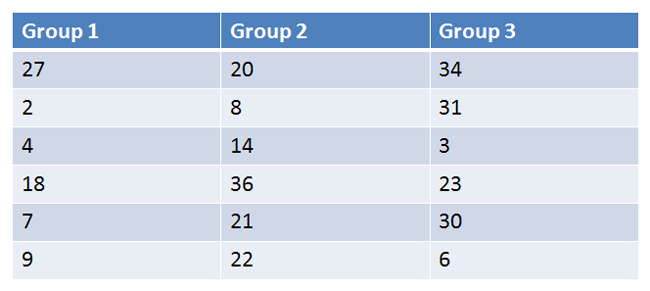
Figure 1.

Let's test to see if there are any differences with a hypothesis test.

Steps for Kruskal-Wallis Test
1. Define Null and Alternative Hypotheses 2. State Alpha 3. Calculate Degrees of Freedom 4. State Decision Rule 5. Calculate Test Statistic 6. State Results 7. State Conclusion

1. Define Null and Alternative Hypotheses

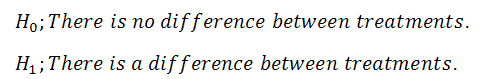
Figure 2.

2. State Alpha

alpha = 0.05

3. Calculate Degrees of Freedom

df = k – 1, where k = number of groups

df = 3 – 1 = 2

4. State Decision Rule

We look up our critical value in the Chi-Square Table and find a critical value of plus/minus 5.99.

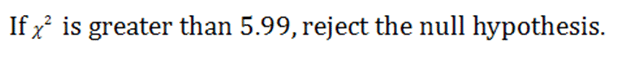
Figure 3.

5. Calculate Test Statistic

First, we must rank every score we have:

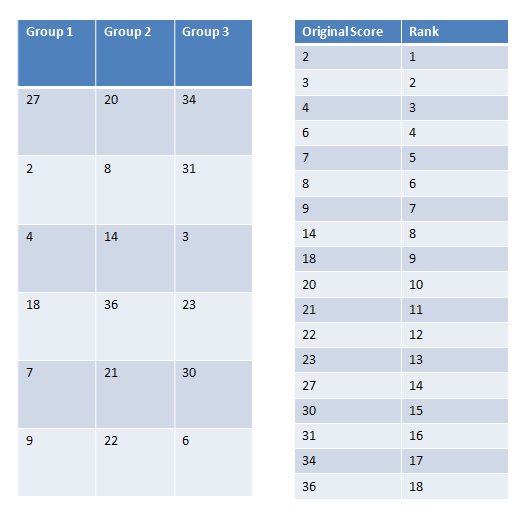
Figure 4.

We then replace our original values with the rankings we've just found:

Figure 5.

An "H" score (think of it as a Chi-Square value) is then calculated using the sums of the ranks of each group:

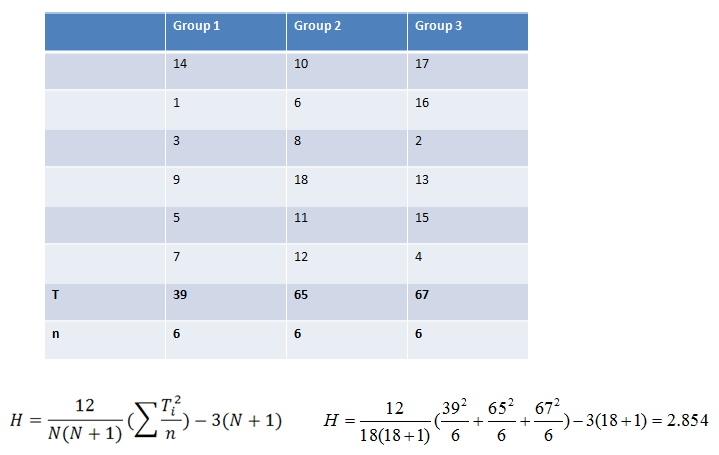
Figure 6.

6. State Results

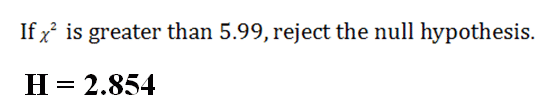
Figure 7.

Do not reject the null hypothesis.

7. State Conclusion

There is no significant difference among the three groups, H = 2.854 (2, N=18), p > .05.

---