| Direct Variation |
|---|
|
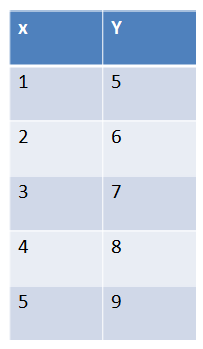
When a value "y" increases as a value "x" increases, direct variation is said to be present. |
Below, "x" and "y" vary directly. As one increases, the other increases.
|
Figure 1. |
|---|
| Inverse Variation |
|---|
|
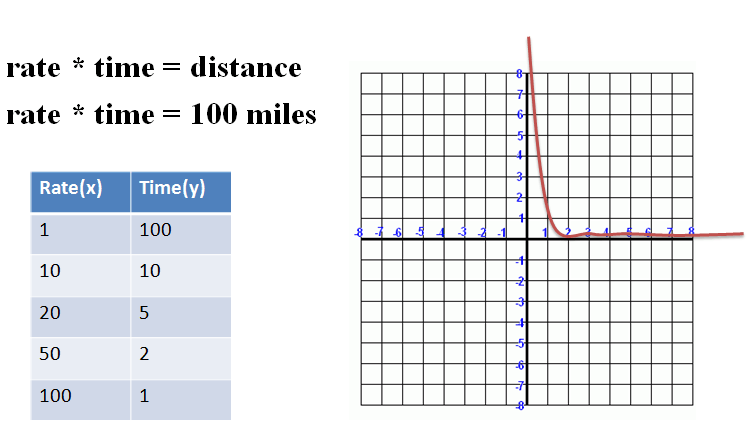
"y" varies inversely with "x" if there is a nonzero constant such that xy = k. |
Here, "rate" and "time" vary inversely at a constant rate. As one increases, the other decreases:
|
Figure 2. |
|---|