Infinite Geometric Series (Jump to: Lecture | Video )

Figure 1.

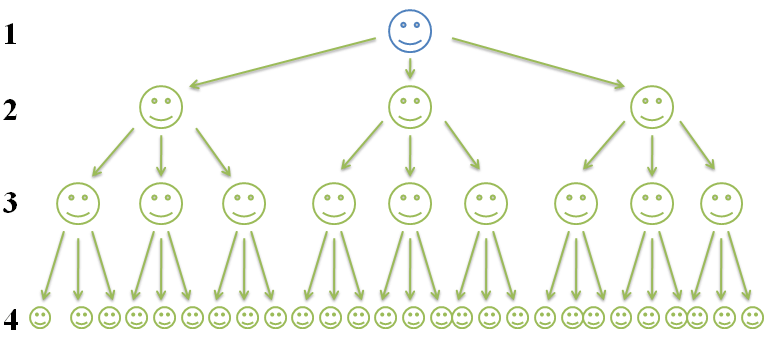
Imagine you have a secret. You tell 3 friends, who each tell 3 friends, who then tell another 3 friends. This is an example of a geometric series.

Geometric Series: 1 + 3 + 9 + 27, r = 3

Here's an example of an Infinite Geometric Series:

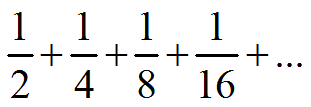
Figure 2.

Each term is half of its previous term, and the series continues forever. How do we find the sum of a series that continues forever?

Sum of an Infinite Geometric Series
The sum of an infinite geometric series is found using the equation: 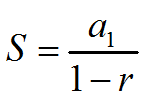when -1 < r < 1

First, we determine r by dividing any term by the term just before it:

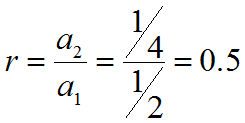
Figure 3.

Now that we have r, we can calculate our sum:

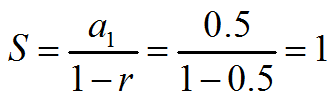
Figure 4.

Our infinite geometric series sums to 1.

The sum of an infinite geometric series only exists if -1 < r < 1.

An infinite geometric series that has a sum is called a convergent series.