Extra Z-Score Problems (Jump to: Lecture | Video )

Here are some extra problems involving z-scores:

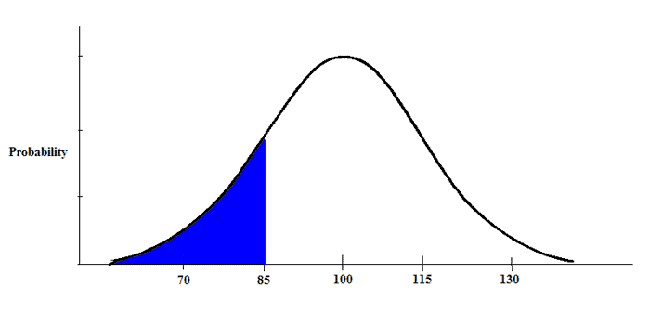
In the United States, the average IQ is 100, with a standard deviation of 15. What percentage of the population would you expect to have an IQ lower than 85?

Figure 1.

Basically, we're trying to find what area corresponds to the blue tail shown above. First, we calculate the z-score.

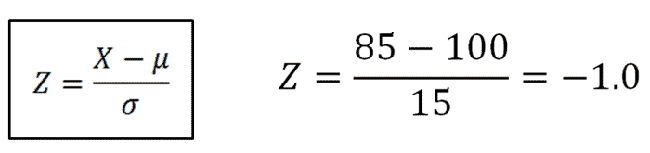
Figure 2.

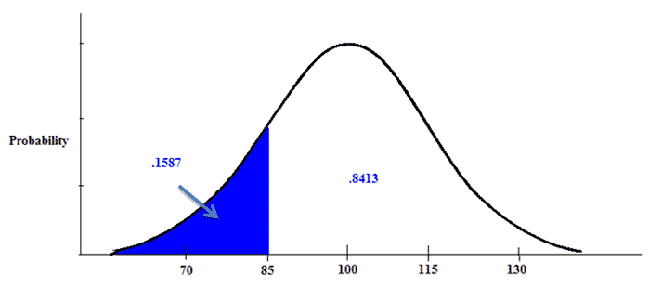
We then look up this z-score in our z-table. After doing so, we find the area in the body is .8413. We subtract that value from 1 to find the area in the tail.

Figure 3.

Our answer is .1587. About 16% of the population has an IQ score lower than 85.

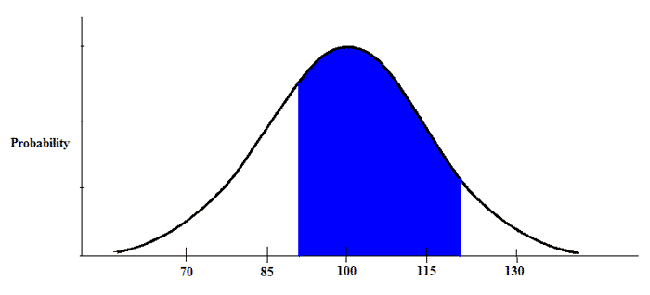
What if the question was like this: In the United States, the average IQ is 100, with a standard deviation of 15. What percentage of the population would you expect to have an IQ between 90 and 120?

Figure 4.

We're trying to find what area corresponds to the blue area shown above. First, we calculate both z-scores.

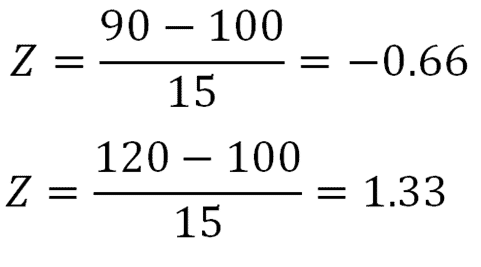
Figure 5.

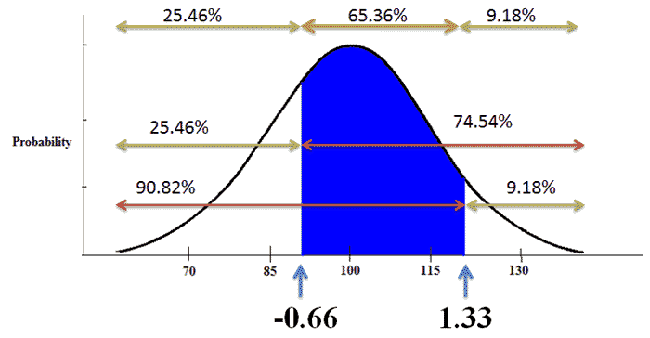
In order to find the area between those two z-scores, we must first look up each z-score in the Z table (click to open). We find that the area in the body for 0.66 is 0.7454, and the area in the body for 1.33 is 0.9082.

Figure 6.

Using this information and what we know about the normal curve, we find that 65.36% of the population has an IQ score between 90 and 120.

---