Equation of a Hyperbola (Jump to: Lecture | Video )

Hyperbola
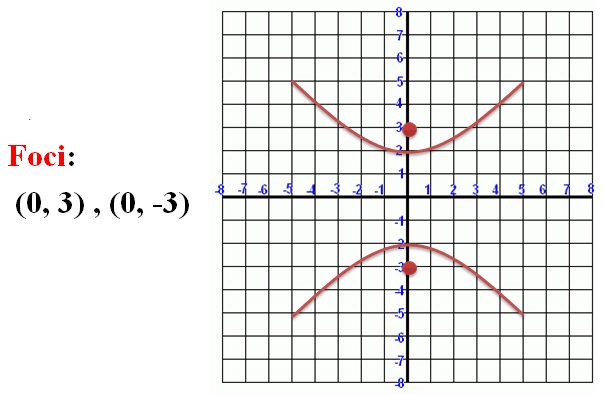
A hyperbola is a set of all points on a plane where the absolute value of the difference of the distances between two fixed points (the foci) is constant.

Below we have a graph of a hyperbola:

Figure 1.

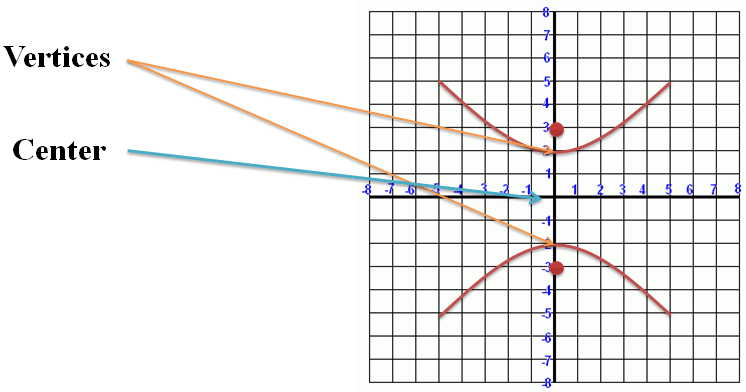
Its vertices are at (0, 2) and (0, -2). Its center is at (0, 0):

Figure 2.

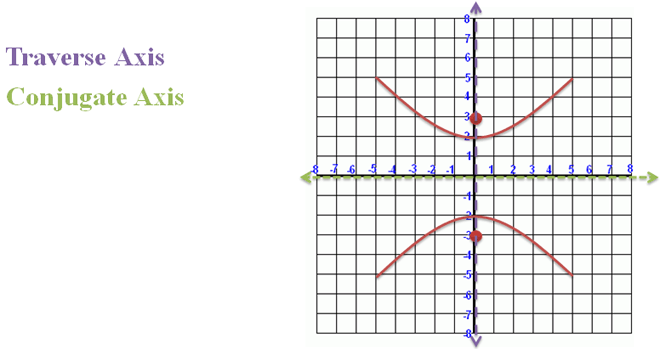
It has a traverse axis, and a conjugate axis:

Figure 3.

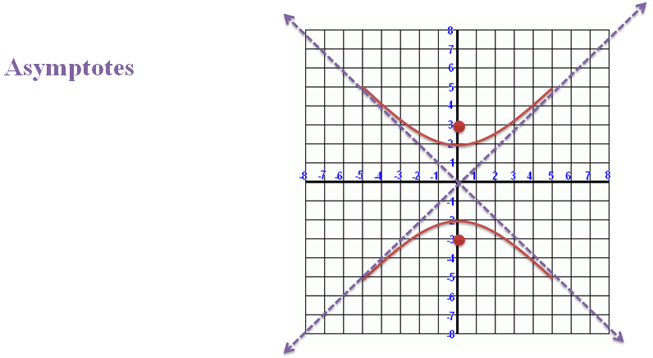
It also has two diagonal asymptotes:

Figure 4.

Equation of an Hyperbola
The equation for a hyperbola depends on if it is horizontal or vertical (as determined by its traverse axis).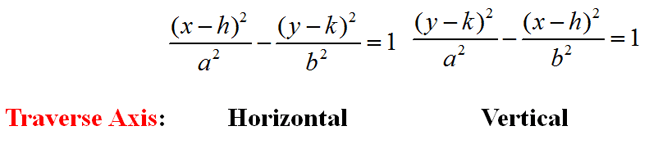

Let's find the equation of our hyperbola.

"c" is equal to the distance of each foci from the center.

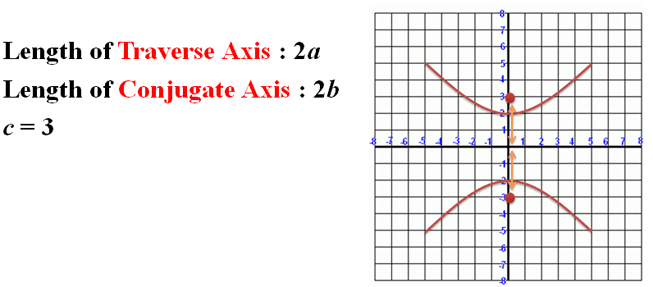
Figure 5.

"a" is equal to the distance of each vertex to the center.

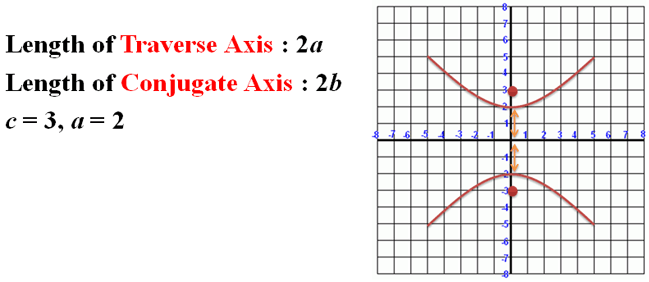
Figure 6.

The Pythagorean Theorem can be used in this situation to determine the missing "b" value.

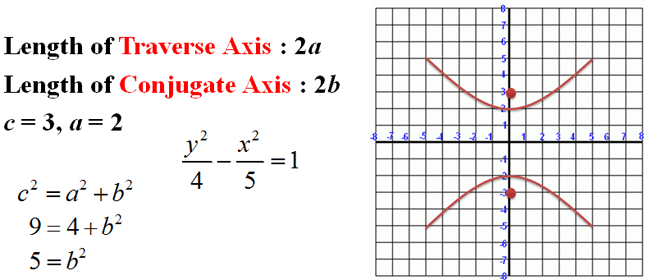
Figure 7.

Now, we plug in our a squared, b squares, and center values to have a final equation for our specific Hyperbola:

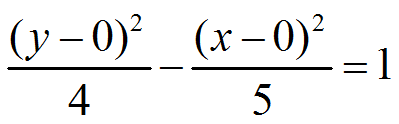
Figure 8.

---