Effect Size (Jump to: Lecture | Video )

Let’s say you know a certain population mean to be 100.

People in Sample A took Medication #1. Sample A has a sample mean of 120. After running your statistics, you find the mean of Sample A to be significantly different from the population mean.

People in Sample B took Medication #2. Sample B has a sample mean of 200. After running your statistics, you find the mean of Sample B to be significantly different from the population mean.

Hypothesis Testing only tells us that each of these samples are different from the population. It does not tell us the strength, or magnitude, of this effect.

After running a statistical analysis, if you reject the null hypothesis it then makes sense to calculate the effect size to determine the strength of the effect. Here's one measure of effect size, cohen's d, using some data I just made up:

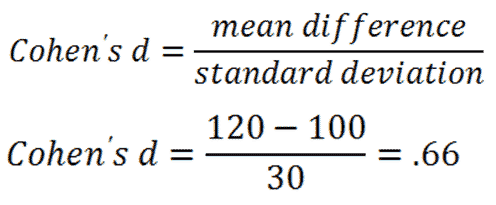
Figure 1.

When using cohen's d, effect sizes are as follows:

d = 0.2, small effect

d = 0.5, medium effect

d = 0.8, large effect

So, in this situation our 0.66 would represent a medium-to-large effect size.