Descartes’ Rule of Signs (Jump to: Lecture | Video )

Fundamental Theorem of Algebra
Every polynomial equation with complex coordinates and a degree greater than zero has at least one root in the set of complex numbers.

A polynomial equation with degree n will have n roots in the set of complex numbers.

How many zeros (and what kinds of zeros) does this equation have?

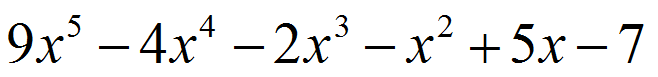
Figure 1.

After arranging the terms of a polynomial equation into descending powers:

The number of positive real zeros in y = P(x) is equal to the number of changes of sign in front of each term, or is less than this by an even number

and

The number of negative real zeros in y = P(x) is the same as the number of changes of sign in front of the terms of P(-x), or is less than this value by an even number.

First, we test for the number of positive real zeros:

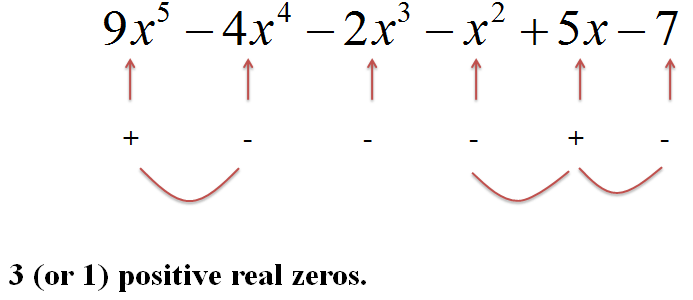
Figure 2.

Second, we test for the number of negative real zeros:

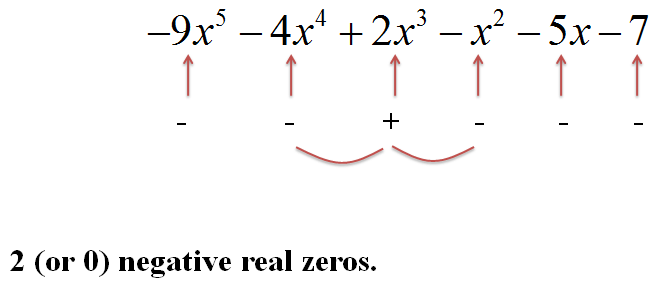
Figure 3.

So, how many different combinations of zeros (and what kinds of zeros) does this equation have?

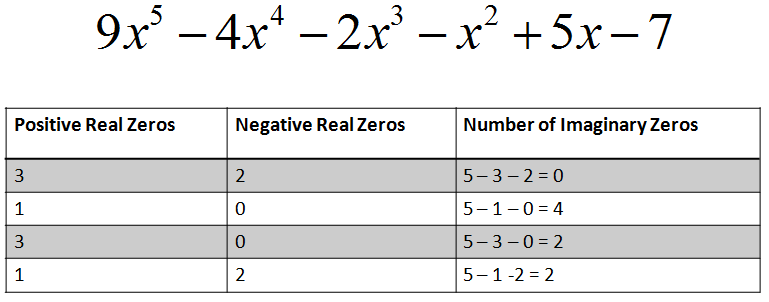
Figure 4.