Confidence Intervals for the Difference of Two Proportions (Jump to: Lecture | Video )

We use the z-Test for Proportions to test if two proportions are different from one another. After the z-test, confidence intervals can be constructed to estimate how large that difference is.

Imagine we already have this data from a previous z-test:

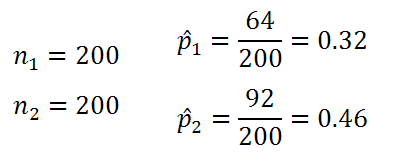
Figure 1.

Construct a 95% confidence interval for the proportion difference.

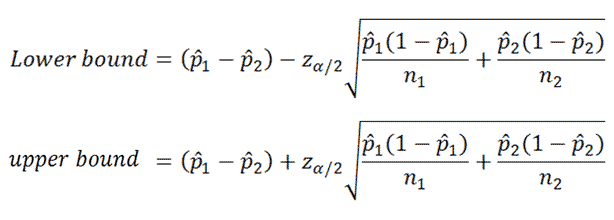
Figure 2.

Above are the equations for the lower and upper bounds of the confidence interval.

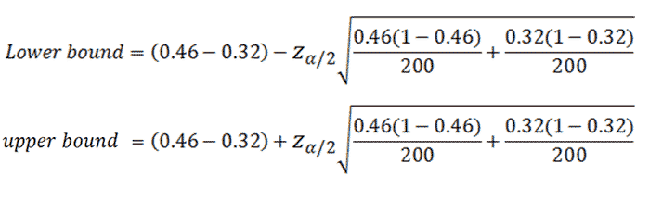
Figure 3.

We already know most of the variables in the equation, but what should we put for z?

We want to create a 95% confidence interval. That means we have an alpha of 0.05(5%) which is split into two equal tails. This 2.5% refers to the value we look up in the z-table in order to find the z-score we need to plug into the equation. When we look up 1 - 0.025, we find a z score of 1.96.

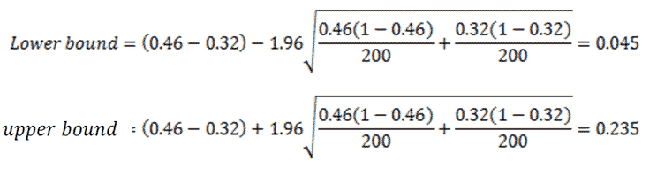
Figure 4.

We are 95% confident that the mean difference between the two proportions is between 0.045 and 0.235.