Confidence Intervals for Population Proportions (Jump to: Lecture | Video )

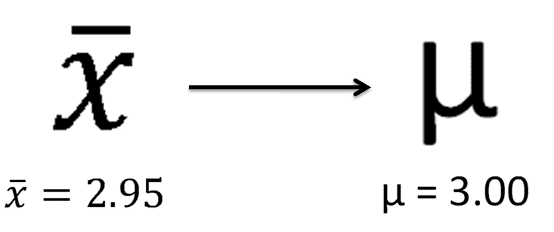
Remember that the value of any statistic that estimates the value of a parameter is called a point estimate.

Figure 1.

Here's an example involving proportions: In a recent poll of 200 households, it was found that 152 households had at least one computer. Estimate the proportion of households in the population that have at least one computer.

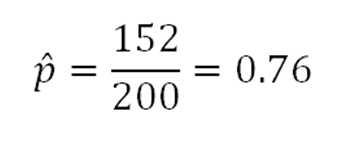
Figure 2.

This is just a single estimate, so it’s probably off from the actual value of the population proportion. Because of this, we’re going to create a confidence interval to give a more realistic impression of what the actual population proportion value may be.

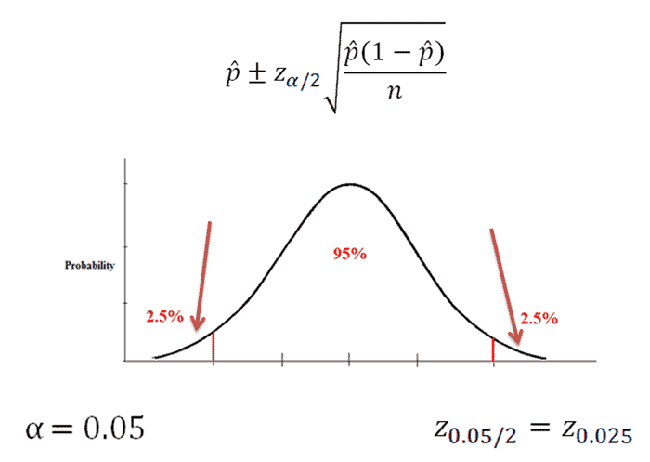
There are two requirements for constructing meaningful confidence intervals about a population proportion:

Figure 3.

Now, let's construct a 95% confidence interval to estimate the previous population proportion.

Figure 4.

We're trying to create 95% confidence interval. That means we have an alpha of 0.05(5%) which is split into two equal tails. This 2.5% refers to the value we look up in the z-table in order to find the z-score we need to plug into the equation. We find a z of "1.96" to plug into the equation.

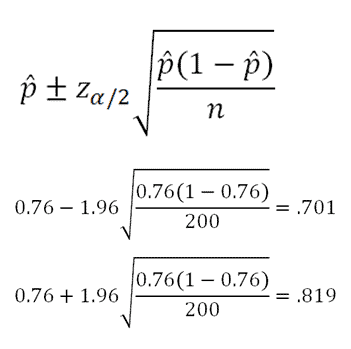
Figure 5.

We are 95% confident that the proportion of households in the population with at least one computer is between .701 and .819.