Central Tendency: Mean, Median, and Mode (Jump to: Lecture | Video )

Central Tendency
Central tendency refers to the measure used to determine the center of a distribution of data. It is used to find a single score that is most representative of an entire data set.

1, 1, 2, 2, 2, 3, 3, 4, 5, 5

If we could pick a single value to represent the above sample data set, what ways could we do it?

Mean
To find the mean, add up all values, then divide by the total number of values you have.

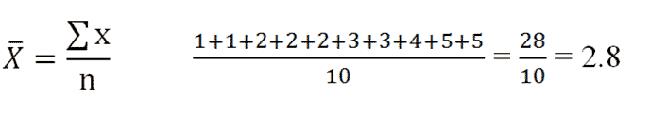
Figure 1.

Our mean is 2.8.

Median
To find the median, first put all the values in order (this has been done already). Next, find out what value lies in the middle.

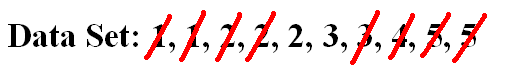
Figure 2.

What happens when there are two values in the middle? Find the median by calculating the mean of the two values. Here, the median is (2 + 3) / 2 = 2.5

Mode
The mode is simply the most frequently occurring value.

For our data set, 2 is the mode because it occurs the most frequently.

If two values occur the most often, the distribution is said to be bi-modal. If more than two values occur the most often, the distribution is said to be multi-modal.

What should you use?

The mean will be used for almost all occasions. However, outliers can sometimes interfere with usage of the mean.

Outlier
An outlier is a value that is very different from the other data in your data set. This can skew your results.

In situations with many outliers, the mean is not a good measure of central tendency. The median or mode should be used instead, depending on the type of information you’re dealing with.

---