| Binomial Experiment |
|---|
|
An experiment is a binomial experiment if: 1. It is repeated a fixed number of times. 2. The trials are independent. 3. Trials have two mutually exclusive outcomes, either success or failure. 4. The probability of success is the same for all trials. |
Try this example: In a recent survey, it was found that 85% of households in the United States have High-Speed Internet. If you take a sample of 18 households, what is the probability that exactly 15 will have High-Speed Internet?
First, let's check if it meets the four conditions:
1. Is this experiment being repeated a fixed number of times?
YES
2. Are the trials independent?
YES, discovering that one home has High-Speed Internet will not affect the probability of other homes having High-Speed Internet.
3. Are there two mutually exclusive outcomes?
YES, a home either has High-Speed Internet(success) or doesn’t have High-Speed Internet(failure). These events cannot occur together so they are mutually exclusive.
4. Is the probability of success the same for all trials?
YES, the probability of success for each trial is 85%.
Now, let's work through the equation. To use this equation, you should already have a pretty good idea about what a combination is.
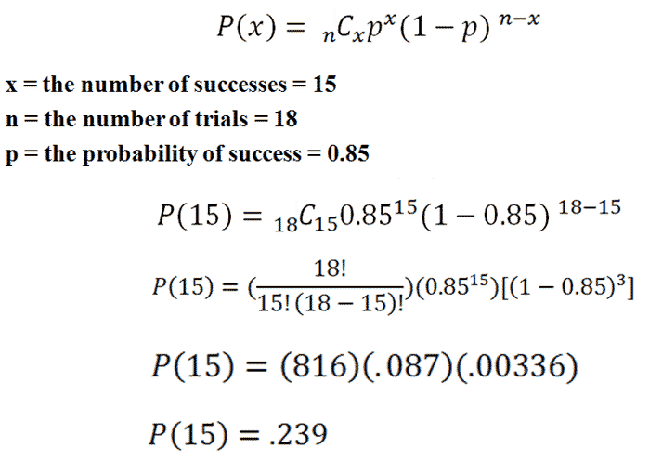
|
Figure 1. |
|---|
By following the above steps, you should find that the probability of 15 households having High-Speed Internet is .239.
What if I changed the example around a little? In a recent survey, it was found that 85% of households in the United States have High-Speed Internet. If you take a sample of 18 households, what is the probability that at least 15 will have High-Speed Internet?
It says "at least" 15, so that means we have to calculate the probabilties for 15, 16, 17, and 18 homes, then add everything together:
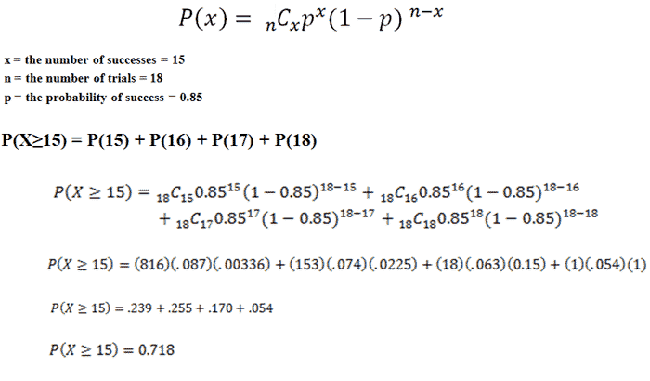
|
Figure 2. |
|---|
By following these steps, you should find that the probability of at least 15 households having High-Speed Internet is .718.